Il premio Nobel per la fisica del 2022 è stato assegnato ad Alain Aspect, John Clauser e Anton Zeilinger “per esperimenti con fotoni entangled, stabilendo la violazione delle disuguaglianze di Bell e aprendo la strada alla scienza dell'informazione quantistica”. Ma questi lavori hanno origini profonde e risalgono alla fine degli anni Venti del secolo scorso, quando Niels Bohr e Albert Einstein si diedero battaglia, a suon di esperimenti mentali, sulle fondamenta della meccanica quantistica originando uno dei più floridi dibattiti della fisica moderna.
Il dibattito
La meccanica quantistica, nella forma in cui viene comunemente presentata, fonda le sue radici nel biennio 1925-1927 grazie agli sforzi intellettuali di alcuni tra i più autorevoli fisici del secolo scorso. Giusto per citare alcuni tra i più famosi: Niels Bohr, attorno al quale prese forma una fiorente Scuola, Werner Heisenberg, Paul Dirac, Max Born, Erwin Schrödinger et cetera. Proprio Bohr ed Heisenberg si resero ideatori di quella che oggi è chiamata interpretazione di Copenaghen della meccanica quantistica, che si basa su alcuni principi di base o postulati:
- La meccanica quantistica è intrinsecamente indeterministica (principio di indeterminazione).
- Il modulo quadro della funzione d’onda di un sistema fornisce la probabilità per i risultati delle misure (regola di Born).
- Non si può osservare contemporaneamente il duplice aspetto di alcune rappresentazioni fisica (e.g. onda-particella) durante il medesimo esperimento (principio di complementarità).

FIG.1 Bohr e Heisenberg all'Istituto di Copenaghen nel 1936. Credits: Niels Bohr Archive
La nozione di indeterminismo, che rappresenta il primo brusco taglio con la fisica classica, venne introdotta nel marzo del 1927 da Heisenberg nel manoscritto intitolato “Sul contenuto intuitivo della cinematica e della meccanica nella teoria quantistica”, dove scrive:
“Noi non abbiamo ipotizzato che la teoria quantistica, in contrasto con quella classica, sia essenzialmente una teoria statistica, nel senso che dai dati forniti in modo esatto si possano trarre solo conclusioni statistiche. Piuttosto, in tutti i casi in cui nella teoria classica esistono relazioni tra grandezze che sono realmente misurabili in modo esatto, anche in teoria quantistica valgono le corrispondenti relazioni esatte. Ma nella formulazione netta del principio di causalità: «se conosciamo in modo preciso il presente, possiamo prevedere il futuro», non è falsa la conclusione, bensì la premessa. In linea di principio noi non possiamo conoscere il presente in tutti i suoi dettagli.” [1]
Il principio di complementarità verrà presentato da Bohr il 16 settembre dello stesso anno al Congresso di Como, mentre l’interpretazione probabilistica del modulo quadro della funzione d’onda fu derivata da Born in un articolo del 1926[2]. Un appunto divertente: nell’articolo la probabilità viene inizialmente presentata come proporzionale alla funziona d’onda della particella; solo successivamente con una nota a piè di pagina aggiunse: “dopo una più precisa analisi, risulta che la probabilità è proporzionale al quadrato della funzione d’onda".
L’interpretazione di Copenaghen tirò a sé diverse critiche e molti furono gli scettici, tra i quali troviamo il tradizionalista e premio Nobel per la fisica Wilhelm Wien. Nel giugno del 1926, quando le due versioni della meccanica quantistica (quella delle matrici di Heisenberg e quella ondulatoria di Schrödinger) erano già dimostrate, Wien tenne un discorso all’Università di Monaco in cui affermava:
“[Mi dispiaccio del tramonto della] massima era in fisica quando la meccanica si era affermata e aveva offerto la possibilità di predire con la massima precisione il moto dei corpi celesti. [La fisica era irrimediabilmente compromessa da un’oscura teoria quantistica che predicava la combinazione di numeri interi secondo certe regole incomprensibili confinati col misticismo numero] Da dove vengano queste regole rimane un mistero, e se doveste avere difficoltà a seguire le mie osservazioni potete sempre confrontarvi al pensiero che non è che i fisici comprendano queste cose molto meglio.” [3]
Anche Paul Dirac, che come già detto fu uno dei protagonisti nella creazione della teoria quantistica, non si tirò indietro nel commentare lo stato delle cose:
“Il problema dell’interpretazione fisica si dimostrò ben più difficile del semplice scrivere le equazioni.” [4]
Ma chi vestì i panni di principale oppositore fu il padre della teoria della relatività: Albert Einstein. Nonostante gli iniziali contributi, e il suo vivo interesse per i suoi sviluppi, le manifestazioni di approvazione di Einstein verso la meccanica quantistica cessarono presto. In accordo con uno dei suoi maggiori biografi [Pais, 1991] le prime manifestazioni di un dissenso permanente risalgono al dicembre del 1926 in una lettera di risposta a Born:
“La meccanica quantistica è degna di ogni rispetto. Ma una voce interiore mi dice che questa ancora non è la soluzione giusta. La teoria ci offre molto ma non ci avvicina al segreto dell’Antico. In ogni caso, sono convinto che non stia giocando a dadi.” [5]
La cosa piuttosto interessante è che lo stesso Einstein accettò che la sua posizione critica nei confronti della meccanica quantistica gli assicurasse che “a Princeton io sia considerato un vecchio pazzo”. [6] Oppure, sempre in una lettera a Born:
“Anche il grande successo iniziale della teoria quantistica non mi fa credere nel gioco dei dadi, anche se sono ben consapevole che i nostri colleghi più giovani lo interpretano come una conseguenza della senilità. Senza dubbio verrà il giorno in cui vedremo quale atteggiamento istintivo era quello corretto.” [7]
Ma fu durante il quinto Congresso Solvay del 1927 che iniziò la sua personale lotta contro l’interpretazione di Copenaghen, dando inizio a quello che è passato alla storia come il dibattito tra Bohr ed Einstein. Il tema scelto per il congresso era “Elettroni e Fotoni” e in molti, se non tutti, aspettavano di sapere la posizione di Einstein sui recenti sviluppi della meccanica quantistica (ricordiamo che il principio di indeterminazione, di complementarità e l’interpretazione probabilistica della funzione d’onda erano stati formulati pochi mesi prima). Dal canto suo Einstein si rinchiuse nel suo silenzio, rifiutando anche l’invito di tenere in quella sede una lezione sulla statistica quantistica (Statistica di Bose-Einstein). Il fisico Otto Stern ci dona un quadro della situazione:
“Einstein scendeva a colazione ed esprimeva i suoi dubbi e ogni volta aveva immaginato qualche bell’esperimento dal quale si vedeva che la teoria non funzionava. Pauli e Heisenberg non prestavano molta attenzione. Bohr, viceversa, ci rifletteva a fondo e la sera, a cena, quando eravamo tutti riuniti, analizzava minuziosamente il problema fino a chiarirlo.” [8]
Le obiezioni di Einstein si concentravano essenzialmente su due punti: contestava che la funzione d’onda ψ forniva una descrizione completa dei processi e criticava l’apparente necessità di una sorta di azione a distanza. In merito scriveva:
“Mi sembra che le difficoltà non possano essere superate a meno che la descrizione del processo in termini di onda di Schrödinger non sia integrata specificando qualche altro dettaglio/particolare sulla posizione della particella. Se uno lavora sono con le onde di Schrödinger l’interpretazione finale contraddice il principio di relatività.” [9]
Prima di iniziare ad esporre uno dei suoi classici esperimenti mentali, Einstein si divertì a dichiarare:
“Devo scusarmi se non ho approfondito a sufficienza la meccanica quantistica.” [10]
Presentò poi una versione alternativa dell’esperimento delle due fenditure. Si prenda un fascio di elettroni che colpisca uno schermo fisso sul quale è presente una fenditura; gli elettroni trasmessi formano la tipica figura di diffrazione, che viene vista su un secondo schermo. Per Einstein la meccanica quantistica non fornisce una descrizione completa dei singoli elettroni in questo tipo di esperimento perché, se abbiamo due punti distinti A e B sullo schermo, so che se un singolo elettrone è arrivato in A allora, istantaneamente, non è arrivato in B. Ma questo implicherebbe una particolare azione istantanea a distanza tra A e B, violando però il postulato della relatività sulla velocità della luce. Inoltre, nota Einstein, che in base all’esperimento di Bothe e Geiger sull’effetto Compton, non c’è limitazione alla precisione con la quale si possono osservare le coincidenze nei processi individuali.
La risposta data a Einstein è che il principio di indeterminazione delimita la quantità massima di informazione che si può ottenere con un determinato apparato sperimentale. Infatti, nell’esperimento di Bothe-Geiger si ottiene una localizzazione spaziale e temporale, ma si rinuncia ad una precisa informazione sull’energia e la quantità di moto. Inoltre, la teoria quantistica afferma che la posizione finale di un singolo elettrone non può essere prevista con certezza, ma che è necessario fare una predizione sulla probabilità che un elettrone arrivi in uno dei due punti dello schermo.
Il dibattito fra i due continuò anche al sesto Congresso Solvay del 1930 sul magnetismo. Questa volta Einstein trovò un ragionamento piuttosto ingegnoso che sembrava confutare il principio di indeterminazione, formulando il famoso Gedankenexperiment (esperimento mentale) del fotone nella scatola.
Si prenda una scatola in cui è stato praticato un foro, che può essere aperto o chiuso tramite un dispositivo controllato da un orologio posto all’interno della scatola stessa. La si riempia di radiazione e infine la si pesi. Regolando il meccanismo di apertura, si può far aprire il foro facendo emettere un singolo fotone. Si ripesi la scatola. Così, almeno in linea di principio, si possono determinare con accuratezza arbitraria sia l’energia del singolo fotone sia, tramite l’orologio, l’istante esatto della sua emissione. Tutto ciò è in pieno contrasto con il principio di indeterminazione di Heisenberg per le variabili energia-tempo. Per Bohr fu un completo shock a cui non sembrava esserci rimedio.
“Per tutta la seria fu estremamente angustiato, e continuava a passare dall’uno all’altro, cercando di persuaderli che non poteva essere, che sarebbe stata la fine della fisica se Einstein avesse avuto ragione; ma non riusciva a trovare un modo di confutare il paradosso.” [11]

FIG.2. Albert Einstein e Niels Bohr immortalati durante il congresso Solvay del 1930. Foto scattata da Paul Ehrenfest.
Ma alla fine ci riuscì perché, citando un capitolo di [Kumar] “Einstein dimentica la relatività”. Fu infatti nella teoria del suo rivale che Bohr trovò l’argomentazione per confutare l’esperimento mentale che tanto lo aveva afflitto. Quando peso inizialmente la scatola, leggo la sua posizione nello spazio grazie a un supporto graduato; la perdita di peso, dovuto alla fuoriuscita del fotone, viene compensata con l’ausilio di un contrappeso agganciato sotto la scatola. Questo peso riporta l’indice del supporto graduato nella posizione iniziale con un’incertezza Δq. Ovviamente anche all’operazione di misura è associata un’incertezza sulla massa Δm. Ma quando aggiungiamo il contrappeso, questo imprime alla scatola una quantità di moto con relativa incertezza Δp che è legata alla Δq dalla relazione ΔpΔq = h. Con varie osservazioni, tra cui la più significativa è che il ritmo di un orologio dipende dalla sua posizione all’interno del campo gravitazionale, Bohr arrivò a una formula del tutto analoga a quella di Heisenberg [12]. Ancora una volta la meccanica quantistica è salva, almeno per ora.
Successivamente Einstein abbandonò la ricerca di contraddizioni e si convinse che, sebbene fosse logicamente coerente, non era la teoria definitiva che Bohr credeva. Insomma, era solo una piccola parte di una verità molto più ampia. Questo si riscontra anche in una lettera indirizzata al Comitato Nobel dove candidò Heisenberg e Schrödinger per il premio, asserendo che:
“È indubitabile, a mio parere, che questa teoria contenga un frammento della verità ultima.” [13]
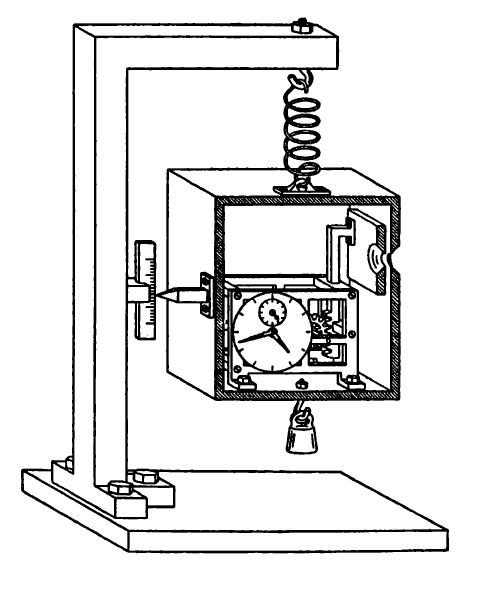
FIG.3. L'apparato sperimentale per l'esperimento mentale di Einstein.
Cambiò allora punto di vista: dal 1931 in poi Einstein si concentrò sull’idea che la meccanica quantistica fosse una teoria incompleta. In questo contesto sviluppò il suo esperimento mentale più duraturo.
Paradosso e realtà
“La meccanica quantistica è magica.” [14]
Dopo i due congressi Solvay si sciolsero le riserve di Einstein per quello che riguardava la coerenza della meccanica quantistica, ma nuovi interrogativi stavano nascendo. Egli era convinto che, nella forma presentata dalla scuola di Copenaghen, la teoria quantistica era una manifestazione di una teoria più generale e più profonda che ancora doveva essere modellata. Quello che lo rendeva più perplesso era il ruolo che funzione d’onda ψ rivestiva: tutto quello che si sa o si può sapere di un sistema fisica, o su un qualsivoglia “pezzo di realtà”, è espresso dalla funzione d’onda.
Nel marzo 1935 nella rivista specialistica Physical Review uscì un articolo firmato da Einstein Podolsky e Rosen (EPR) destinato a diventare celebre: “Can quantum-mechanical description of physical reality be considered complete?” (La descrizione quantomeccanica della realtà fisica può essere considerata completa?). Qui gli autori sostenevano che la meccanica quantistica non era in grado di fornire una descrizione completa della realtà fisica.
Einstein già in quegli anni era diventato un personaggio di pubblico dominio e anche la stampa trattò l’argomento. Il 4 maggio 1935 il New York Times pubblicò un articolo con un titolo leggermente sensazionalistico: “Einstein attacca la teoria quantistica. Lo scienziato e due colleghi trovano che è incompleta anche se corretta.”

FIG.4. Il titolo del New York TImes del 4 maggio 1935. Credits by Institute for Advanced Study.
L’articolo EPR inizia introducendo un’ipotesi di realtà dei fenomeni fisici:
“Qualsiasi considerazione seria di una teoria fisica deve tener conto della distinzione tra la realtà oggettiva, che è indipendente da qualsiasi teoria, e i concetti fisici cin cui la teoria opera. Nel tentativo di giudicare il successo di una teoria fisica possiamo porci due domande: «la teoria è corretta?» e «la descrizione fornita dalla teoria è completa?». Solo nel caso in cui si possono dare risposte positive a entrambe le domande i concetti della teoria possono considerarsi soddisfacenti. La correttezza della teoria si giudica dal grado di accordo tre le conclusioni della teoria e l’esperienza umana. Questa esperienza in fisica assume la forma di esperimenti e misurazioni.” [15]
Continua poi introducendo quello che viene denominata condizione (o criterio) di completezza e spiegando cosa sia un elemento della realtà:
“Ogni elemento della realtà fisica deve avere un equivalente nella teoria fisica. Gli elementi della realtà fisica non possono essere determinati da considerazioni filosofiche a priori, ma devono essere trovati facendo riferimento ai risultati di esperimenti e misurazioni (…) Se, senza in alcun modo disturbare il sistema, possiamo prevedere con certezza (cioè con probabilità uguale ad uno) il valore di una quantità fisica, allora esiste un elemento della realtà fisica corrispondente a questa quantità fisica.” [16]
Quindi, se esisteva anche un solo elemento della realtà fisica che non veniva spiegato dalla teoria, questa era da essere considerata, per forza di cose, incompleta. Il [Kumar] dona un esempio molto esplicativo e paragona la situazione a una persona che trova un libro in una biblioteca e quando chiede informazioni il bibliotecario risponde che non ce n’è traccia all’interno del database. Ma siccome il libro ha tutte le caratteristiche che indica che fa parte di quella biblioteca, l’unica spiegazione possibile è che il catalogo della biblioteca sia incompleto.
Prima di andare a commentare il contenuto vale la pena aprire una piccola parentesi: all’interno dell’articolo sono presenti alcune parole chiave (come, ad esempio, “misurazione”) che devono essere inseriti all’interno di un determinato contesto. Bohr sottolineava già da diversi anni l’importanza e la cautela nell’uso del linguaggio quando i fenomeni coinvolgevano gli effetti quantistici. Questo, infatti, rivestiva un ruolo di primaria importanza. Nel 1948 disse:
“Locuzioni che ricorrono sovente nei lavori dei fisici, come «perturbazione dei fenomeni per via dell’osservazione», rappresentano un uso di parole come ‘fenomeni’, ‘osservazioni’ e ‘misura’, scarsamente compatibile con l’uso comune e con la definizione pratica, e quindi atto a generare confusione. Per un più corretto modo di esprimersi è giusto richiedere con forza che la parola fenomeno venga usata esclusivamente per indicare osservazioni in circostanze ben precise, comprensive di un resoconto dell’intero esperimento.” [17]
Ritornando al contenuto, può risultare interessante (o almeno pedagogico) presentare l’argomento EPR con un esempio “piuttosto umano”, ideato da due giganti della fisica italiana: Giorgio Salvini e Oreste Piccioni:
“Trattavamo, nel nostro esempio banale, le particelle come se fossero esseri umani, macroscopici.
Pietro ed Andrea sono due gemelli. Sono stati generati insieme e costituiscono, prima di separarsi, uno stato preciso, con le loro lance 1,2 orientate in modo opposto (un fisico direbbe, con spin o memento angolare totale uguale a zero). Ed ecco che Pietro ed Andrea si separano uno dall’altro, senza alcun particolare tormento di forze esterne. Supponiamo di tracciare una linea retta che li colleghi e supponiamo che ciascuno dei due abbandoni la sua lancia su quella linea, partendo da una posizione perfettamente verticale. La posizione finale assunta da ciascuno lancia dopo la caduta sarà a sinistra o a destra della linea che abbiamo tracciato prima: ognuna delle due possibilità avrà una probabilità [P] del 50%.
Sin qui va tutto bene. Ma attenzione, ecco il punto inatteso di sorpresa: mentre localmente la probabilità P è aleatoria ([P] Sinistra= [P] Destra), le regole della meccanica quantistica prevedono che la posizione della lancia caduta di Andrea dipende dalla posizione di caduta assunta da Pietro. Le coppie di probabilità relative alle lance dei due fratelli non sono indipendenti, ma bensì solo correlate (correlazione EPR). Come se ognuno dei due potesse conoscere, a grandissima distanza, come è caduta (a sinistra o a destra) la lancia dell’altro.
Ma che sciocchezza è questa, dice il fisico classico, dotato di classico buonsenso e non esperto di quantistica. Che ne sa Andrea, ormai lontano, di quanto è accaduto ed è stato misurato su Pietro. Ormai i due sono scorrelati e indipendenti uno dall’altro. Invece no! Nel mondo microscopico governato dalla meccanica quantistica le cose vanno proprio così: il modo di manifestarsi di Andrea (lancia a destra o sinistra) dipende dal fatto che Pietro è risultato, nella misura fatta su di lui, con la lancia in quel certo modo. Se direte che questo è un paradosso, e che questo può essere la buccia di banana sulla quale l’apparato della meccanica quantistica può cadere, non sarete soli: si chiama Paradosso di Einstein-Podolsky-Rosen. Naturalmente è un paradosso che si estende alle particelle elementari, non ad oggetti infinitamente complessi, classici, come Pietro ed Andrea.” [18]
Nell’articolo originale viene invece proposto il seguente esperimento mentale. Siano date due particelle A e B supposte interagenti, il cui stato è caratterizzato dall’impulso totale e dalla loro distanza relativa. A un certo istante di tempo le separiamo e quando sono sufficientemente lontane andiamo a misurare (compiere un’osservazione). Se decidiamo di misurare la posizione la posizione di A, si può predire con certezza la posizione di B senza disturbarla con gli strumenti di misura dato che ora le due sono poste a grandissima distanza. La stessa cosa vale per la misura della quantità di moto. Allora per la definizione data, questi saranno elementi di realtà. Ma la meccanica quantistica (o meglio il principio di indeterminazione) ci dice che impulso e posizione di A non possono essere simultaneamente elementi della realtà perché le due variabili non commutano. Questo in letteratura è conosciuto con il nome di paradosso EPR.
Allora Einstein dice che ci sono due possibilità. La prima è che l’informazione viene istantaneamente trasferita in modo tale che la particella B assuma una determinata configurazione, ovvero un certo valora della posizione/quantità di moto a seconda di quello che viene misurato in A, ma questo violerebbe il principio di Relatività. Oppure B possedeva già valori determinati ancora prima che la misura decidesse quale delle due grandezze corrispondenti di A andare a controllare. La naturale conseguenza secondo Einstein et al. è che la meccanica quantistica è una teoria incompleta perché non è in grado di descrivere la realtà in toto ma soltanto alcuni suoi aspetti.
La visione critica di Einstein può essere ulteriormente capita leggendo nell’articolo del 1936 dal titolo “Physik und realität”, dove scrisse:
“Io cerco di spiegare come mai la meccanica quantica non appare in grado di dare un fondamento pratico alla fisica: ci si trova implicati in contraddizioni, se si tenta di considerare la descrizione teorica quantica come descrizione completa del singolo sistema o evento fisico.” [19]
Appena fu pubblicato l’articolo fece risuonare l’allarme tra i principali pionieri della teoria quantistica. Secondo la testimonianza del fisico Leo Rosenfeld (a quel tempo impiegato con Bohr alla prima formulazione quantistica del campo elettromagnetico) la pubblicazione dell’articolo EPR fu un vero e proprio fulmine a ciel sereno sopra Copenaghen. Per ordine di Bohr tutti i lavori della Scuola furono interrotti e gi sforzi rivolti alla risposta da dare nella forma più rapida e convincente. Questa prese forma nell’articolo dell’ottobre 1935 pubblicato sulla stessa rivista e con lo stesso titolo di quello EPR[20] dove Bohr affermò che non si può parlare di proprietà di singole particelle anche quando queste sono poste a grandi distanze le une dalle altre.
Chi reagì positivamente fu invece Erwin Schrödinger che per primo si rese conto che alla base del paradosso EPR c’è il concetto di stato entangled. Difatti, in una lettera indirizzata ad Einstein egli usò il termine tedesco “verschränkung”, che venne poi tradotto in inglese come entanglement (e che in italiano può essere tradotto con il termine intrecciato): “la funzione d’onda totale dopo l’interazione e la separazione spaziale dei due sistemi non permette di descrivere questi due come singoli, ma devono considerarsi ancora come un sistema unico. I due sistemi si possono ritenere separati e indipendenti solo dopo che è intervenuto un atto di misura, cioè solo dopo che c’è stato un collasso della funzione d’onda che distrugge l’entanglement.” [21]
Dal suo articolo del 1935:
“Quando due sistemi, di cui conosciamo gli stati attraversi i rispettivi rappresentanti, entrano in interazione (fisica) temporanea a causa delle forze conosciute tra loro, e quando dopo un certo periodo di influenza reciproca i sistemi si separano di nuovo, allora non possono più essere descritti nello stesso modo di prima. Non lo chiamerei uno, ma piuttosto il tratto caratteristico della meccanica quantistica, quello che ne sancisce il suo completo allontanamento dalle linee di pensiero classiche. Con l’interazione le due funzioni ψ sono diventate entangled.” [22]
È interessante leggere la reazione di Wolfgang Pauli, il padre del principio di esclusione. In una lettera a Heisenberg scrisse:
“Einstein ha fatto ancora una volta una dichiarazione sulla meccanica quantistica (…) Come è noto, è un disastro ogni volta che accade- ma poi aggiunse un commento come solo lui poteva fare- Se uno studente in uno dei suoi primi semestri avesse sollevato tali obiezioni, lo avrei considerato abbastanza intelligente e promettente.” [23]
C’è qualcosa che si nasconde?
Ritorniamo all’idea di realtà data nell’articolo di Einstein, Podolsky e Rosen seguendo la linea di pensiero di [Forte, Rottoli]. Il realismo locale impone che, per particelle che sono casualmente disconnesse, non ci sono conseguenze sulla prima in relazione a quello che viene fatto sulla seconda e viceversa. Quindi una proprietà che può essere misurata è necessariamente posseduta dal sistema ancora prima che la misura abbia luogo. Per i tre questo risulta essere “un principio irrinunciabile”.
Quindi, dato che la meccanica quantistica contraddice il realismo locale (come visto sopra) ne segue che la teoria è incompleta. Ma questa ci dice un ulteriore fatto. Se, ad esempio, andiamo a misurare il numero quantico di spin di due particelle e troviamo che per la prima abbiamo uno stato su, obbligatoriamente si trova che per la seconda particella lo stato è quello giù (per il principio di esclusione di Pauli). Questa parte leggermente tecnica ci fa giungere a un risultato interessante: sembra che qui venga violato il tanto citato realismo locale perché c’è trasferimento di informazione istantaneo. Qui ci vengono in soccorso i “calzini di Bertlmann.”
“Il dottor Bertlmann ama indossare calzini di colore diversi per il piede destro e per il piede sinistro. È impossibile prevedere quale colore avrà a un dato piede in un dato giorno, ma quando vediamo che il primo calzino è rosa, siamo già certi che il secondo avrà un colore diverso. L’osservazione di un calzino unita alla conoscenza delle abitudini di Bertlmann, ci dà immediatamente un’informazione sul secondo. E la questione EPR non è forse la stessa cosa?” [24]
Questo però ci dice che uno stato EPR “è uno stato che corrisponde a certi, e non altri, eventi possibili e nel fatto che questi eventi possano avvenire in punti casualmente disconnessi.” [25]
Ma la realtà è che non è possibile che il sistema prima della misura possieda una certa proprietà perché questa dipende da ciò che decidiamo di misurare e il sistema non può possedere simultaneamente le diverse proprietà che potremmo decidere di misurare. È quindi solo dopo che si misura, ad esempio, lo spin della prima particella che la seconda acquisisce di conseguenza un valore ben definito.
Per concludere, un modo per non rinunciare al realismo locale e contemporaneamente accettare la proposta EPR era quella della cosiddetta teoria delle variabili nascoste che vide in David Bohm uno dei maggiori esponenti.
CONTINUA NEL PROSSIMO NUMERO
Note:
Boffi S. p.72-73.
Born M.
Cassidy D. p.133.
Pais A. (1993) p. 265.
The Collected Papers of Albert Einstein, p. 403.
Kumar, p. 304.
Ibidem, p. 318.
Pais A. (1991) p. 473.
Wick D. p. 54
Ibidem, p.53
Pais A (1991) , p.475.
INFN
Pais A. (1991) p.477.
Mermin D. N. (1985)
Einstein, Podolsky, Rosen.
Ibidem
Pais. A (1991) p. 485
Salvini G.
De Martini F.
Bohr N. (1935)
Di Giuseppe G., p.9
Schrödinger (1935)
Kumar, p.309
Bell p. 184
Forte, Rottoli p. 320
Bibliografia:
Bell J. (2010) I calzini di Bertlmann e la natura della realtà in Dicibile e Indicibile in Meccanica Quantistica (Adelphi, traduzione a cura di Gabriele Lorenzini).
Bohr N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev, 48, 696.
Boffi S. Il Principio di Indeterminazione. Quaderni di fisica teorica (Università degli studi di Pavia).
Born M. (1926) On the quantum mechanics of collision. Zeitschrift für Physik (37), 863-67.
Cassidy D.C. (1996), Un’estrema Solitudine. La vita e l’opera di Werner Heisenberg (Bollati Boringhieri).
Cini M. (2004) Oreste Piccioni e il Paradosso EPR Rend. Fis. Acc. Lincei s. 9, v. 15:393-399.
Di Giuseppe G. Interferometria quantistica mediante stati entanled generati da fluorescenza parametrica.
De Martini F. (92004) Il paradosso EPR Rend. Fis. Acc. Lincei s.9, v 15:401-410.
Einstein A. Podolsky B. e Rosen N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47,77.
Forte S., Rottoli L. (2018) Fisica quantistica (Fisica Zanichelli).
Greco P. (2020) Quanti. La straordinaria storia della meccanica quantistica (Carrocci editore).
INFN Scatola di Luce di Einstein: http://www.lnf.infn.it/edu/incontri/2015/slides-corso-fisica-moderna/11m....
Kumar M. (2009) Quantum. Einstein, Bohr and the great debate about the nature of reality (W. W. Norton & Company).
Mermin D.N. (1985) Is the moon there when nobody looks? Realitu and the quantum Theory. Physics Today 38, 4, 38.
Pais A. (1993), Il danese tranquillo. Niels Bohr, un fisico del suo tempo 1885-1962 (Bollati Boringhieri. Traduzione a cura di Daniel Canarutto).
Pais A. (1991), “Sottile è il Signore…”. La scienza e la vita di Albert Einstein (Bollati Boringhieri. Traduzione di Tullio Cannillo).
Salvini G. (2004) La vita di Oreste Piccioni e la sua attività scientifica in Italia Rend. Fis. Acc. Lincei, s.9, v 15:289-324.
Schrödinger E. (1935) Discussion of Probability Relations between Separated Systems. Mathematical Proceedings of the Cambridge Philosophical Society, 31(4), 555-563.
The Collected Papers of Albert Einstein, Volume 15: The Berlin Years. Writings & Correspondence, June 1925-May 1927 (English Translation Supplement).
Wick D. (1995) The Infamous Boundary. Seven Decades of Heresey in Quantum Physics (Springer).

